lunes, 31 de agosto de 2015

Matemática en la antigua China


31 de Agosto del 2015, Clase 6: Matemática en la antigua China

      Es inhabitable que la cultura asiática me parezca intrigante en muchos aspectos, supongo que la mayoría de occidente lo vea de una manera similar. Veamos por ejes;

 - Ubicación 
- Sintaxis
- Curiosidades
1. Ubicación:

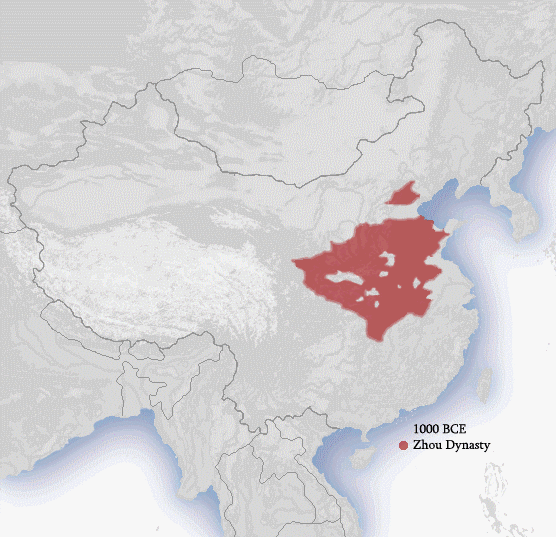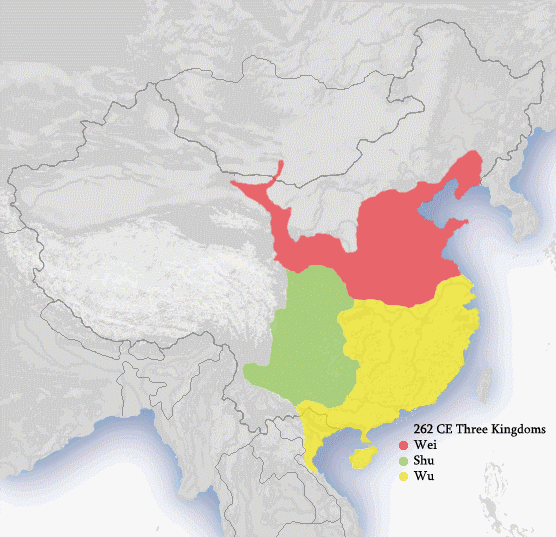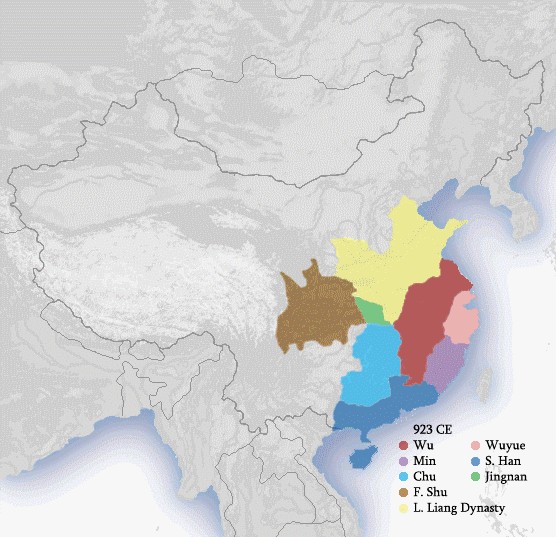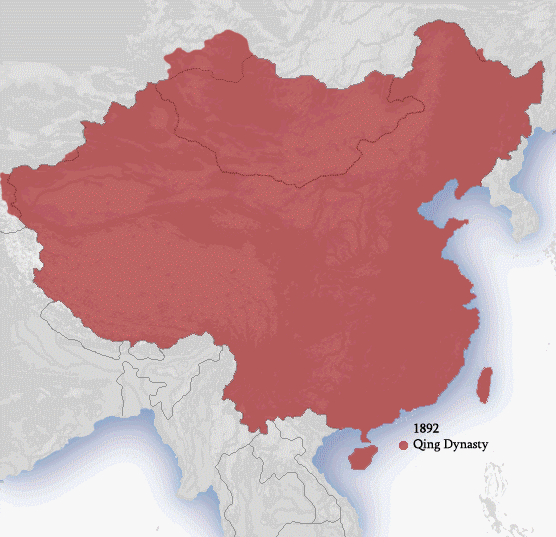
 Me encontré este mapa político animado en wikipedia acerca de las dinastías en la historia de china: 
Territories of Dynasties in China

 Pojanji from wikipedia [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/)], via Wikimedia Commons



2. Sintaxis:

     A decir verdad no es tan extrabagante como en otras culturas pero si muy útil, muy semejante al sistema indio-arábico en cuanto al uso posicional de los símbolos. Abordaban de manera mas explicita los números negativos y en cuanto al cero no tenían en símbolo que lo representara, dado a que simplemente dejaban  un espacio para indicar la existencia de una posición sin volar numérico.
Veamos:

3. Curiosidades

 3.1 Cuadros mágicos:

        La longevidad y la protección era el significado de la tortuga, que evitaba los desbordes de los ríos. En el cuadriculado de su caparazón se utilizaban números donde se inspiraron los primeros cuadros mágicos:

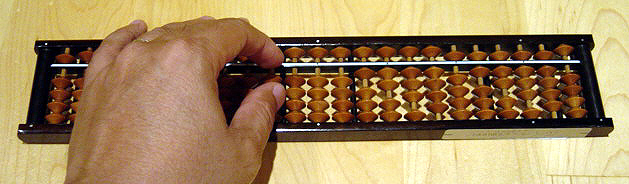
3.2. Sorobán:

       Es un instrumento utilizado para mejorar la deducción a partir de la observación, con el cual se logran hacer cálculos numéricos con cifras muy altas a tiempos muy reducidos.
Soroban
Sorobán japonés. Las 10 columnas de la derecha muestran el número 1234567890.

   

Publicadas por a la/s No hay comentarios.:

lunes, 24 de agosto de 2015

Aportes de la escuela Pitágorita desde a la perspectiva sur africana

24 de Agosto del 2015, Clase 5: Aportes de la escuela Pitágorita desde a la perspectiva sur africana

     Ciertamente el aspecto teórico formal de la matemática no fue tan abordado por parte de los pueblos africanos, mas el uso práctico que ellos le dan a las matemáticas es digno de señalar, vamos a definir nuestros ejes:

- Ubicación geografía
- Matemática 

1. Ubicación geográfica 

     La parte sur del continente africano:



2. Matemática

      En las historia de las matemáticas de dicha región se encuentran varias curiosidades entre ellas este hueso:

      Con alrededor de 20000 años de antigüedad el hueso de Ishango en sus distintas marcas refleja conteo en base 12.

      Más hacia nuestra época, gracias a los estudios de Paulus Gerdes, se conocen diferentes formas de aplicación del teorema de Pitágoras en los tejidos utilizados en las ropas y otros utensilios de la región sur africana. Ejemplo de esto son los botones entrelazados de Mozambique:


 

También las redes de puntos de equidistantes:

Por mi parte recomendarles Paulus Gerdes como autor de libros de énfasis matemático alusivos a la cultura sur americana.
3. Referecias



Publicadas por a la/s No hay comentarios.:

lunes, 17 de agosto de 2015

Grecia Antigua: La matemática desde la perspectiva occidental


17 de Agosto del 2015, Clase 4: La matemática desde la perspectiva occidental


     La matemática griega es la mas conocida y estudiada en el occidente, esto a muchos les lleva a la mente la palabra Pitágoras. Pero antes de entrar en calor definamos los ejes:

     - Posición geográfica
     - Detalles culturales y políticos
     - Matemáticas

1. Posición Geográfica

     Veamos un video que explica mejor las tierras que abarcaba la Grecia antigua ubicada entre 1200 a.c hasta el 146 a.c. 



     El sur Italia, Asia menor, Macedonia y Ática son puntos que me llaman especialmente la atención, por ejemplo, tenían influencia de la región europea actual y de la región asiática, Macedonia iba ver nacer a Alejandro Magno en el 356 a.c, el que sería instruido por Aristóteles y que llegaría a ser el rey de los conquistadores; y finalmente la Ática por su fidelidad a la diosa Atena en relación con lo que hoy es la actual capital de Grecia, Atenas.


2. Detalles culturales y políticos

     Los hombres nativos que eran dueños de tierras son los únicos considerados ciudadanos. Las personas con importancia social no tenia derechos especiales, es decir, nacer una familia reconocida implicaba beneficios. El estatus social lo definía el poder económico por ello alguna podía cambiar su estatus si ganaba mucho dinero o viceversa. La educación era principalmente privada aunque si existieron escuelas publicas. Al rededor de los seis años los niños iniciaban su preparación en lectura, escritura, canto y manejo de algún instrumento, a los doce se agregaba lucha, lanzamiento de disco, jabalina y carrera. A los dieciocho al concluir sus estudios algunos iniciaban su entrenamiento militar y unos muy pocos adinerados continuaban sus estudios con algún maestro famoso o amor pederástico.



3. Matemáticas

     Los aportes matemáticos relacionados a los griegos se atribuyen principalmente a los nombres de fundadores de escuelas famosas de la antigua Grecia, como lo es el caso de la escuela de Pitágora o de Platón. Se destaca:


3.1 Números Perfectos:

  "Un número perfecto es un número natural que es igual a la suma de sus divisores propios positivos, sin incluirse él mismo." 

                                                                    28= 14+7+4+2+1

Un dato que me pareció interesante es la representación binaria de los números perfectos: 













3.2 Números Amigos:

     Dos números amigos son dos números enteros positivos a y b tales que la suma de los divisores propios de uno es igual al otro número y viceversa, es decir σ(a)=b y σ(b)=a, donde σ(n) es igual a la suma de los divisores de n, sin incluir a n.

              σ(220)=  1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110, sumados son igual a 284.
              σ(284)=   1, 2, 4, 71 y 142,                                  sumados son igual a 220.


3.3 Teorema de Pitágoras:
      
     "La suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa".





3.4 Intervalos musicales, Afinación Pitágorica:

    El siguiente video explica como descubrió esto:


A los que quieran profundizar más:



4. Referencias:








Publicadas por a la/s No hay comentarios.:

lunes, 10 de agosto de 2015

La matemática babilónica

10 de Agosto del 2015, Clase 3: Matemática Babilónica


      Para mí parecer los babilónicos manejaban una matemática muy adelantada para el siglo XVIII a.c, Como es usual definiré ejes de para el presente análisis:

     - Posición geográfica
     - Detalles culturales y políticos
     - Sintaxis numérica
     - Curiosidades


1. Posición geográfica:

       El imperio babilonio controlaba gran parte de lo que hoy es Irak, Iran y Siria, Al comunicar a Egipto con Mesopotamia se hicieron maestros en el comercio y en la matemática que eso implica,


2. Detalles culturales y políticos:

      La primera dinastía babilónica fue Amorrea fundada alrededor de 1894 a.c, y presentaba una estructura política usual a la época imperial con una infraestructura de palacios y ciudades. Bajo este esquema regían códigos y leyes, uno de los más conocidos es el código de Hammurabi que establecía:

  -- La jerarquización de la sociedad: existen tres grupos, los hombres libres o "awilum", los "mushkenum" (quienes se especula podrían ser siervos o subalternos) y los esclavos o "wardum".

  -- Los precios: los honorarios de los médicos varían según se atienda a un hombre libre o a un esclavo.

  -- Los salarios: varían según la naturaleza de los trabajos realizados.

  -- La responsabilidad profesional: un arquitecto que haya construido una casa que se desplome sobre sus ocupantes y les haya causado la muerte es condenado a la pena de muerte.

  -- El funcionamiento judicial: la justicia la imparten los tribunales y se puede apelar al rey; los fallos se deben plasmar por escrito.

  -- Las penas: aparece inscrita una escala de penas según los delitos y crímenes cometidos. La base de esta escala es la Ley del Talión.

      


  3. Sintaxis numérica:
      
   Usando palillos con forma de un prisma triangular ponían marcas en la tablas de arcilla que formaban la siguiente simbología: 


     
     

4. Curiosidades:

     4.1 Los escribas:
            
             Estos fueron personajes adoptados por la influencia egipcia que son seleccionados desde niños para educarse aprender a leer y a escribir jeroglíficos y pictografía además de conocer los secretos del cálculo.
           
             Se encargaban de llevar la cuentas de las familias adineradas usando las típicas tablillas, En la actualidad se conservan tablillas que muestran ejercicios de geómetra para el calculo de área y otras aplicaciones practicas.  
      

     4.2 Marcador de posición:

                 El sistema numérico que se utilizaba era posicional, algunos historiadores consideran que el afán que tenían los babilonios por contarlas estrellas los llevo a buscar una manera de representar números extraordinariamente grandes y lo encontraron dando con el valor relativo a posición del numero. Esto los llevo a un fenómeno en su sintaxis, cuando un contador no tenia representación numérica se dejaba un espacio: rondando así el descubrimiento del cero, el cuál no seria considero un número propiamente dicho hasta más de 1000 años más tarde.
     

     4.3 Ecuaciones Cuadráticas:

                  Unos de los ejercicios más clásicos en la matemática babilónica fue el calculo de un área de una terreno rectangular, la metodología que utilizaban se explica en el siguiente vídeo:
                   




    



     4.4 Teorema de Pitágoras ? Números irracionales:

                  Para terminar con este repaso de la matemática babilónica voy a rescatar la tablilla más polémica que se mantiene en la actualidad:


         

                   Se dice que en ella hay un conocimiento claro del teorema que Pitágoras propusiera varios siglos después y aún mas intrigante que los números en la tablilla son una aproximación de 4 decimales exactos a la raíz cuadrada de 2 que como sabemos es un números irracional. Solo para refrescar estos las dinastías babilónicas se ubican en un rango temporal del XVII a.c al 627 a.c. 




5. Referencias:







Publicadas por a la/s No hay comentarios.:

lunes, 3 de agosto de 2015

Matemática Egipcia

3 de Agosto del 2015, Clase 2: Matemática Egipcia


     La clase de la Matemática Egipcia lleno mis expectativas, para resumir voy analizar de manera general cada cultura voy hablar en dos ejes:

     - Sintaxis numérica
     - Curiosidades


1. Sintaxis numérica:

      Es claro que no vamos a abordar todas la sintaxis egipcias, simplemente abordaré a los temas según una importancia subjetiva.

     El sistema numérico egipcio no era posicional, es decir, pueden escribir los números de derecha a izquierda, de izquierda a derecha, de arriba a abajo o abajo a arriba que el numero expresa el mismo valor, la orientación de los símbolos era meramente estética.  Dividiremos los símbolos en números enteros y decimales.
 
    1.1 Números Enteros:

            1.1.1 Descripción:
        


           1.1.2 Ejemplos:

                                                   
V20 V20 V1 V1 V1
V20 V20 V1 V1 V1
Z1 Z1 Z1 Z1
Z1 Z1 Z1 Z1
 = 640

                                                                 V20
                                                                 V20		V1M12   = 1120                          


    1.2 Números Decimales:

            1.2.1 Descripción:

D11
= \frac{1}{2}
D12
= \frac{1}{4}
D13
= \frac{1}{8}
D14
= \frac{1}{16}
D15
= \frac{1}{32}
D16
= \frac{1}{64}

         

                                           



 1.2.1 Ejemplos:


Z1
D12
D13
D15
= 1 + 1/4 + 1/8 + 1/32 = 0.03125


1. Curiosidades:
Calculo del volumen de la pirámide cortada:







Publicadas por a la/s No hay comentarios.:
Suscribirse a: Entradas (Atom)